Preguntas y problemas de cuadriláteros. 1º de bachillerato.

 A continuación colocamos preguntas de teoría y problemas de cara a una prueba escrita, y que vamos a impartir. Pero antes de presentar las preguntas y problemas viene bien leer los tres párrafos que vienen a continuación:

  Los problemas se pueden descargar ya con las soluciones en este enlace:  https://drive.google.com/file/d/1aa_oA5rRQa2sWCU1J492TlG9tFZNuIHu/view?usp=sharing

 Se pueden descargar los enunciados de los problemas con datos  en este enlace https://drive.google.com/file/d/1rPC5x9fw70MzwsSYszJJgkbDX68IOWwR/view?usp=sharing

  Se pueden ver más problemas resueltos de cuadriláteros en el siguiente enlace de este mismo blog: https://dibutodo.blogspot.com/2021/10/mas-problemas-de-cuadrilateros-1-de.html

PREGUNTAS DE CUADRILÁTEROS.

1. Definición de cuadrilátero.

2. Clasifica de forma general los cuadriláteros. 

3. Clasificación de paralelogramos. Señala dos características que sean específicas de ellos.

4. Clasificación de trapecios. Señala dos características que sean específicas de ellos.

5.¿Qué es un trapezoide? 

6. Señala una característica específica de las diagonales de los paralelogramos.

 

7. ¿A qué llamamos bases del un trapecio? 

 

8. ¿Todos los rectángulos posibles se pueden inscribir en una circunferencia? Contesta solo sí o no.

 

9.  ¿Una circunferencia se puede inscribir en un rectángulo? Contesta sí o no.

PROBLEMAS DE CUADRILÁTEROS. 

 
En todos los problemas se pide nombrar todos los vértices.

Construcción de  un cuadrado conocido el lado.

1. Sobre una semirrecta se traza el segmento AB, lado del cuadrado que nos dan.
2. Se levanta una recta perpendicular por el extremo A del segmento AB.
3. Con centro en el extremo A y radio AB se traza un arco para llevar la medida a la prependicular antes trazada, de tal forma que obtenemos el vértice D del cuadrado
4. Basta con trazar un arco de radio AB y de centro en el extremo D y otro con centro en el extremo B para determinar en el corte de los dos arcos el vértice C. 

5. Teniendo los cuatro vértices ya podemos obtener el cuadrado.

Construcción de  un cuadrado conocida la diagonal.

 

 

El problema también podría enunciarse como "construción de un cuadrado conocido el radio de su circunferencia circunscrita o dividiendo euna circunferencia en cuatro partes iguales"

1. Se traza un segmento AC con el valor de la diagonal.
2. Se traza otro diámetro DB perpendicular a la diagonal AB por su punto medio o bien se traza simplemente la mediatriz del segmento AC.
3. Con centro en el punto de corte de las dos diagonales se traza una circunferencia de diámetro AC. Donde corte la circunferencia a la mediatriz obtendremos los puntos DB, vértices del cuadrado.
4. Basta con unir los vértces para resolver el cuadrado solución.

 

Construcción de un rectángulo, conocidos los lados AB y AD.

 

 1. Se traza una semirrecta siendo el extremo A unos de los vértices del rectángulo.
2. Se traza otra semirrecta perpendicular a la anterior por dicho extremo A.
3. Se pasan las medidas de los lados a dichas semirrectas, obteniéndose los vértices B y D.
4. El vértice C se puede obtener de muchas formas; por ejemplo, trazando un perpendicular por el extremo B y colocando la medida igual a DA.
5. Al unir los vértices, obtendremos el rectángulo solución.

 

Construcción de  un rectángulo conocidos un lado AB y la diagonal AC

1. Se traza el segmento AB conocido.
2. Se averigua el rectángulo con la medida AB, que será uno de los catetos y el valor de la diagonal que nos dan, la cual será la hipotenusa, siendo el vértice B de 90º. Obtenemos así el punto C, punto de intersección del arco trazado con centro en A y la perpendicular trazada desde l vértice B.
3. Basta con trazar una paralela desde A al segmento BC y otra paralela por C al segmento AB para obtener el vértice D del rectángulo solución.


Construcción un rombo de lado AB y diagonal AC.

 

 

1. Trazamos el segmento AB, lado del rombo.

2. Construimos el triángulo ABC, con el valor del lado y de la diagonal AC por el método de construcción de un triángulo conocidos los tres lados.

3. Hallamos el otro vértice, bien trazando paparelas a los dos lados ya hallados, bien trazando una paralela por el vértice C al segmento AB, bien colocando en dicha paralela la magnitud del lado.

 

 Construcción de un rombo conocidas la altura  y una diagonal

 

 1. Se traza una semirrecta de extremo el punto A, que será uno de los vértices del rombo.

2. Se levanta la altura dada partiendo de la semirrecta y se traza una paralela a dicha semirrecta a la distancia de esa altura.

3. Con centro en el extremo A y con radio igual a la diagonal que nos han dado, trazamos un arco de circunferencia que cuando corta a la paralela nos determina el vértice C del rombo.

4. Las diagonales de un rombo son perpendiculares entre sí y se cortan en su punto medio. Basta con trazar la mediatriz de la diagonal AC para determinar en la semirrecta y en la paralela trazada los vértices D y B. 

Construcción de un romboide conocidos los lados AB, AD y el ángulo del vértice A.

1. Se traza una semirrecta de extremo el punto A y se coloca en ella el valor del lado del rombo AB.

2. Se traza en el extremo A el ángulo que nos dan.

3. Se coloca sobre el lado del ángulo la medida del lado AD.

4. Por el vertice B se traza una paralela al lado AD y por el vértice D una paralela al lado AB. Donde se cortan dichas paralelas estrá determinado el vértice C del romboide.

 

 Construcción de un romboide conocidos el lado AB, la altura correspondiente a dicho lado y el ángulo del vértice A.

 

1. Se traza una semirrecta de extremo el punto A y se coloca en ella el valor del lado AB.

2. Sobre la semirrecta se levanta la altura que nos dan y se traza una paralela a la semirrecta (o al lado AB) con la distancia de esa altura.

3. Se construye el ángulo que nos dan en el extremo A del lado AB.

4. En la intersección del lado del ángulo del vértice A con la paralalea trazada se encontrará el vértice D del romboide.

5. Basta llevar sobre la paralela la medida del lado AB , sindo uno de los extremos el vértice D para hallar el romboide.

 

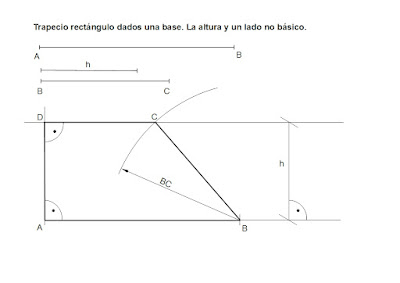
Construye un trapecio rectángulo dados la base AB, la altura y el lado no básico BC.

 

1. Se traza una semirrecta de extremo el punto A y se coloca en ella el valor de la base dada AB.

2. Se levanta la altura dada partiendo de la semirrecta y se traza una paralela a dicha semirrecta a la distancia de esa altura.

3. Con centro en el extremo B y con radio igual al lado BC que nos han dado, trazamos un arco de circunferencia que cuando corta a la paralela nos determina el vértice C del trapecio.

4. El trapecio que nos piden es rectángulo. Basta con trazar una recta perpendicular por el vértice A para hallar el vértice D del trapecio.

 

 Construcción de un trapecio isósceles conocidas las dos bases AB y CD , y la altura h.

 

 1. Se traza una semirrecta de extremo el punto A y se coloca en ella el valor de la base AB del trapecio.

2. Se levanta la altura dada partiendo de la semirrecta y se traza una paralela a dicha semirrecta a la distancia de esa altura.

3. Se traza la mediatriz de la base AB del trapecio. La cual nos servirá para repartir la medida de la base CD en la recta paralela, por igual y a un lado y al otro lado de la mediatriz, ya que el trapecio es simétrico, y determinar los vértices C y D.

 

 Construcción de un trapecio escaleno conocidas las dos bases AB  y CD , la diagonal AC. Dicha diagonal forma 45º con la base AB.

 

 

1. Se traza una de las bases AB. y se traza el ángulo (de 45º) que forma la diagonal dada sobre el vértice A.

2. Se traslada sobre esa diagonal la medida AC, determinándose así el vértice C.

3. Por el vértice C se traza una paralela a la base AB. Recordemos que las bases de un trapecio son paralelas entre sí.

4. Sobre dicha paralela se traslada el valor de la base CD que nos dan, obteniéndose así el vértice D.

 

 Construcción de un trapezoide conocidos los cuatro lados; AB , BC, CD, DA y la diagonal AC.

Un trapezoide se hace generalmente por triangulación, es decir,  colocando triángulos adyancentes con los datos que nos dan. 

1. Se traza el lado AB, y se traza el triángulo que resulta de las medidas del lado AB y las diagonales AC y BC. Así obtendremos el vértice C del trapezoide.

2.Sobre la diagonal AC, que es uno de los lados del triángulo anterior ya resuelto, se traza otro triángulo de lados el valor de la diagonal AC y los lados DA y CD, obteniéndose el vértice D.