EL DOMINIO DEL DIBUJO
Blog educativo del Departamento de Dibujo para el alumnado de E.S.O. y Bachillerato del IES Álvar Núñez, de Jerez de la Frontera.
Las imágenes son todas del autor del blog menos las que llevan información CCO a pie de foto
jueves, 25 de septiembre de 2025
viernes, 19 de septiembre de 2025
CONTENIDOS DE LA MATERIA DE DIBUJO TÉCNICO DE 4º E SO.
Del currículo oficial se hará, durante este curso, especial incapié en los siguientes saberes básicos:
1. PROPORCIONALIDAD.
Razón de proporción
Concepto de proporción.
Reglas de proporción: cuarta, media y tercera proporcional.
2. EQUIVALENCIA
Equivalencia. Concepto. Resolución de problemas.
3. SEMEJANZA.
Semejanza. Concepto. Aplicación en figuras a escala. Concepto de escala, tipos y escalas gráficas.
4.TRANSFORMACIONES PLANAS.
Transformaciones geométricas en el plano. Identidad, traslación, giro, simetría axial, simetría central, homotecia directa.
5. TANGENCIAS Y ENLACES.
Concepto de tangencia. Problemas de tangencias de rectas tangentes a circunferencia, de circunferencias tangentes entre sí y de circunferencias tangentes a recta y circunferencia.
Enlaces derivados de las tangencias. Aplicaciones en la configuración de piezas industriales
6. GEOMETRÍA DESCRIPTIVA. INTRODUCCIÓN.
Tipos de proyección y de sistemas de representación y su aplicación.
7. SISTEMA DIÉDRICO DE PROYECCIÓN
Sistema diédrico: representación de punto, recta y plano.
Sistema diédrico: Relaciones entre elementos: intersecciones, paralelismo y perpendicularidad.
Proyecciones diédricas de sólidos geométricos sencillos.
8 SISTEMA AXONOMÉTRICO Y DE REPRESENTACIÓN EN CABALLERA.
Sistema axonométrico, ortogonal y oblicuo.
Perspectivas isométrica y caballera. Representación de sólidos geométricos sencillos.
9. SISTEMA CÓNICO.
Sistema cónico: fundamentos y elementos del sistema. Perspectiva frontal. Representación de sólidos geométricos y
espacios sencillos.
10. NORMALIZACIÓN, ACOTACIÓN.
Escalas y formatos. Representación del entorno según finalidad.
Concepto de normalización. Las normas fundamentales UNE e ISO.
Representación de cuerpos y piezas industriales sencillas. Vistas principales.
Acotación. Tipos de líneas y grosores.
Aplicación del lenguaje técnico en la creación de un proyecto tridimensional, desde el boceto hasta la materialización
miércoles, 22 de mayo de 2024
Ejercicios de homología y afinidad. 2º de Bachillerato
1. Presentamos una hoja de ejercicios en blanco sobre ejercicios de homología y afinidad. Tiene especial interés el ejercicio nº 11.
2. Presentamos otro ejercicio. la segunda parte del ejercicio se muestra muy confusa y resolver esa confusión es un buen entrenamiento.
miércoles, 17 de abril de 2024
TA 121. Construcción de un reloj de sol.
A continuación mostramos las indicaciones para resolver un reloj de sol vertical.
Se pide dibujarlo en una hoja gruesa, a escala 2/1.
jueves, 3 de noviembre de 2022
miércoles, 12 de octubre de 2022
TC7. Polígonos regulares. Definición, propiedades, clasificación y construcción.
1. Definición.
Decimos que un polígono es regular cuando tiene todos los lados y los ángulos iguales.
2. Propiedad fundamental.
Todos los polígonos se pueden inscribir en una circunferencia. La circunferencia se llama circunscrita.
3. Clasificación.
Se clasifican según el número de lados. Pongamos algunos ejemplos.
De tres lados: triángulo equilátero.
De cuatro lados: cuadrado.
De cinco lados: pentágono regular.
De seis lados: hexágono regular.
De siete lados: heptágono regular.
De ocho lados: octógono regular.
De nueve lados : eneágono regular.
De diez lados: decágono regular.
De once lados: undecágono regular.
De doce lados: dodecágono regular.
Hay más polígonos con más lados, pero solo hemos mencionado hasta el de doce lados.
4. Construcción.
Se pueden construir de dos formas: que los tengamos que construir a partir del lado o que tengamos que construirlos a partir de su circunferencia circunscrita.
4.1. Construcción de polígonos regulares conocido el lado.
Vamos a dar solo los cuatro casos que vamos a hacer en la lámina. Ofrecemos los enunciados así como los vídeos explicativos sobre su construcción.
4.1.1. Construcción de un triángulo equilátero dado el lado = 70 mm.
https://www.mongge.com/ejercicios/11927
4.1.2. Construcción de un cuadrado dado el lado= 60 mm.
https://www.mongge.com/ejercicios/21215
4.1.3. Construcción de un pentágono regular dado el lado = 40 mm.
(En el vídeo aparece con un lado de 60 mm, pero da igual. En la lámina se hará con el lado de 40 mm)
https://www.mongge.com/ejercicios/3824
4.1.4. Construcción de un hexágono regular dado el lado= 35 mm.
https://www.mongge.com/ejercicios/46846
4.2. Construcción de polígonos regulares conocida la circunferencia que lo circunscribe.
Para esto lo único que hay que hacer es saber dividir una circunferencia en partes iguales. Al unir las divisiones con segmentos obtendremos el polígono.
Vamos a dar solo los cuatro casos que vamos a dibujar en la lámina. Ofrecemos los enunciados así como los vídeos explicativos de su construcción.
4.2.1. Construcción de un hexágono regular conocido el radio de su circunferencia circunscrita = 40 mm.
https://www.mongge.com/ejercicios/17967
4.2.2. Construcción de un heptágono regular conocido el radio de su circunferencia circunscrita = 40 mm.
https://www.mongge.com/ejercicios/9654
4.2.3. Construcción de un octógono regular conocido el radio de su circunferencia circunscrita = 40 mm.
https://www.mongge.com/ejercicios/46813
4.2.4. Construcción de un decágono regular conocido el radio de su circunferencia circunscrita = 40 mm.
https://www.mongge.com/ejercicios/26092
AHORA NOS TOCA DIBUJAR A NOSOTROS.
ACTIVIDAD Nº1.
Título: Construcción de polígonos regulares conocido el lado.
Consiste en resolver en una lámina de formato A/4, con margen y casillero los cuatro ejercicios del apartado 4.1.
Se dividirá la lámina en cuatro partes iguales y se hará cada polígono en cada casillero, colocando el enunciado del ejercicio en la parte superior de cada casillero, con un pautado de 10 mm.
Ofrecemos un ejemplo resuelto por los alumnos. Las líneas auxiliares no se ven muy bien por están dibujadas a lápiz y son muy finas, pero si miramos bien, veremos que se ha hecho el procedimiento en cada uno de los dibujos.
ACTIVIDAD Nº2.
Título: Construcción de polígonos regulares conocida la circunferencia circunscrita.
Consiste en resolver en una lámina de formato A/4, con margen y casillero los cuatro ejercicios de
ACTIVIDAD Nº2.
Título: Construcción de polígonos regulares conocida la circunferencia circunscrita.
Consiste en resolver en una lámina de formato A/4, con margen y casillero los cuatro ejercicios del apartadol apartado 4.2.
Se dividirá la lámina en cuatro partes iguales y se hará cada polígono en cada casillero, colocando el enunciado del ejercicio en la parte superior de cada casillero, con un pautado de 10 mm.
Ofrecemos un ejemplo resuelto por los alumnos. Las líneas auxiliares no se ven muy bien por están dibujadas a lápiz y son muy finas, pero si miramos bien, veremos que se ha hecho el procedimiento en cada uno de los dibujos.
ACTIVIDAD Nº3. DE AMPLIACIÓN.
Título: Construcción de polígonos regulares conocido el lado, II.
Consiste en resolver en una lámina de formato A/4, con margen y casillero.
1. Construir un triángulo equilátero conocida la altura = 50 mm.
2. Construir un cuadrado conocida la diagonal = 70 mm.
3. Construir un hexágono conocido el apotema = 30 mm.
4. Construir un heptágono conocido el lado = 30 mm.
ACTIVIDAD Nº4. DE AMPLIACIÓN.
Título: Construcción de polígonos regulares conocida la circunferencia circunscrita, II.
Consiste en resolver en una lámina de formato A/4, con margen y casillero los tres ejercicios siguientes.
1. Construir un pentágono regular conocido el radio de su circunferencia circunscrita = 40 mm.
2. Construir un decágono regular conocido el radio de su circunferencia circunscrita = 40 mm.
3. Construir un eneágono regular conocido el radio de su circunferencia circunscrita = 40 mm.
martes, 27 de septiembre de 2022
TC6. Cuadriláteros. Primer ciclo de ESO.
1. Definición de cuadrilátero.
Cuadrilátero es un polígono de cuatro lados.
2. Designación.
Los cuadriláteros se designan generalmente por sus vértices, los cuales se escriben con mayúsculas y con las primeras letras del abecedario. Estos vértices también sirven para nombrar los ángulos. Se ordenan generalmente en sentido contrario a las agujas del reloj.
Los lados se nombran generalmente con los propios nombres de los vértices. Por ejemplo: lado AB.3. Propiedades comunes de todos los cuadriláteros.
La suma de sus ángulos siempre es de 360 grados.
Tienen dos diagonales, las cuales son segmentos que unen vértices opuestos.
4. Clasificación de cuadriláteros.
Según la disposición de los lados, los cuadriláteros se clasifican en:
4.1. Paralelogramos: tienen los lados dispuestos paralelos dos a dos. Estos son:
El cuadrado, con lados y ángulos iguales y de 90 grados.
El rectángulo con lados paralelos iguales y ángulos de 90 grados.
El rombo, de lados iguales y ángulos opuestos iguales.
Y el romboide, de lados paralelos iguales y ángulos opuestos iguales.
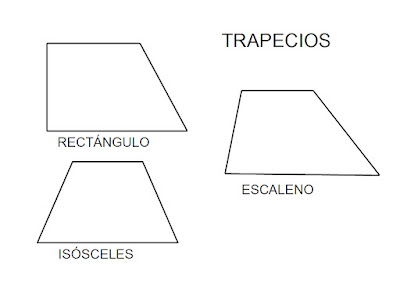
4.2. Trapecios: solo dos de sus lados son paralelos y reciben el nombre de bases. Los otros dos no son paralelos. Estos son: el trapecio rectángulo, con uno de sus lados no paralelos perpendicular a las bases, el trapecio isósceles, con sus lados no paralelos iguales entre sí, y el trapecio escaleno, de lados no paralelos desiguales.
4.3. Trapezoides: son cuadriláteros que no tiene ninguno de sus lados paralelos entre sí.
5. Construcción de cuadriláteros.
5.1. Construir un rectángulo conocidos un lado AB= 60 mm y una diagonal AC= 70 mm.
Vídeo explicativo: https://youtu.be/_WZKihcJBDI
5.2. Construir un rombo dadas las dos diagonales AC= 60 mm y BD= 40.
En el vídeo explicativo a la diagonal AB la llama D y la la diagonal BD la llama d: https://youtu.be/EPdUb97i07E
5.3. Construir un romboide dado el lado AB=50 mm, el lado AD= 35 mm y el ángulo A= 60º.
Ver vídeo: https://youtu.be/fYeSpVH82Qw
5.4. Construir trapecio isósceles dada la dos bases AB=70 mm y CD= 40 mm, así como la altura=35 mm.
Ver vídeo:https://youtu.be/0ixbqVl85qU
También está muy claro el problema en este vídeo: https://youtu.be/8O7K1XUXHm0
ACTIVIDAD Nº 1.
La actividad consiste en dividir un formato A/4 con margen y casillero en cuatro partes iguales y en cada una de ellas dibujar los cuatro problemas que se han visto en el apartado anterior. Se deberá colocar el enunciado en la parte superior de cada dibujo con un pautado de dos a tres renglones a 7 mm de distancia.
Mostramos un ejemplo sobre cómo han de quedar los dibujos. Se ven poco los trazdos pues están hechos a lápiz y contrastan poco:
ACTIVIDAD Nº 2, DE AMPLIACIÓN.
La actividad consiste en dividir un formato A/4 con margen y casillero en cuatro partes iguales y en cada una de ellas dibujar los cuatro problemas que vienen a continuación. Se deberá colocar el enunciado en la parte superior de cada dibujo con un pautado de dos a tres renglones a 7 mm de distancia.
1. Construir un trapecio rectángulo conocidos la base AB= 55mm, la altura= 30 mm y un lado no básico BC=35 mm. (Salen dos soluciones)
2. Construir un trapecio conocidos el lado AB= 75 mm, el lado BC= 45 mm, la diagonal AC= 60 mm y el lado CD= 35 mm.
3. Construir un rombo conocidos un lado =50 mm y uno de los ángulos= 60º.
4. Construir un romboide conocidos el lado AB= 55 mm, el lado BC= 40 mm y la altura correspondiente al lado AB= 30 mm.